Buoyant Force

If an iron object is immersed in water, it displaces $4 \mathrm{kg}$ of water. How much is the buoyant force acting on the iron object in newton?

Match column I with column II and select the correct option from the given codes.

A small metallic piece weighs $50 \mathrm{g}$ and its volume is $20 {\mathrm{cm}}^3$. It is immersed in water. Calculate the

(a) the density of the metallic piece and

(b) upthrust on the metallic piece.

How can you determine the volume of an irregular solid?

Measurement of the volume of an irregular objects is done with the help of 

What is the principle of floatation ? Explain.

What is the application of buoyancy?

What is flotation principle explain with example?

Two metal pieces when immersed in liquid experience equal upthrust on them, then :

A metal sphere is dipped in water. If at $0 °\mathrm{C}$& $4 °\mathrm{C}$ the buoyancies in water are ${\beta }_1$ and ${\beta }_2$ respectively, then :

A block of wood of length $20 \mathrm{cm}$ and area of cross-section $5 {\mathrm{cm}}^2$, floats in water with $\frac{2}{5}$ of its length above water.

Calculate: (i) Density of wood (ii) Weight of wood (iii) Extra force required to completely submerge it in water.

Explain how a submarine dives and resurfaces.

A cubical object of side $2 \mathrm{m}$ and density $200 \mathrm{kg}/{\mathrm{m}}^3$ is floating on water. Calculate the depth of the body in meters that is immersed in water. Take density of water as $1000 \mathrm{kg}/{\mathrm{m}}^3$.

An ice berg of density $900 \mathrm{kg} {\mathrm{m}}^{-3}$ is floating in water of density $1000 \mathrm{kg} {\mathrm{m}}^{-3}$. The percentage of volume of ice-cube outside the water is

An ice berg of density $900 \mathrm{kg} {\mathrm{m}}^{-3}$ is floating in water of density $1000 \mathrm{kg} {\mathrm{m}}^{-3}$. The percentage of volume of ice-cube outside the water is

A wooden cube float in the water is partially immersed. When $200 \mathrm{g}$ weight is put on the cube, it getS further immersed by $2 \mathrm{cm}$. What is the length of the side of the cube?

What are the applications of principles of flotation?

A spring balance A reads $2$ kg with a block of mass m suspended from it. Another balance B reads $3$ kg when a beaker with a liquid is put on its pen. The two balances are now so arranged that the hanging mass m is fully immersed inside the liquid in the beaker as shown in the figure. In this situation

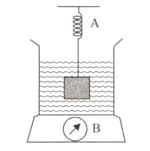
The height of $h$ does not change when the object X is released into the liquid from the X and Y bodies, which are in equilibrium as in the figure the height '$h$decreases when Y is dropped in the liquid.

Which of these statements are correct?

1. The density of body X is greater than the density of the liquid.

2. The density of body Y is greater than the density of the liquid.

3.  The density of body X is smaller than the density of body Y.

The body K of mass m is in equilibrium in the same liquids as in Figures I, II and III.

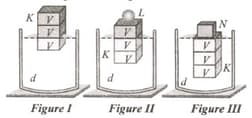
Ratio of mass L to mass N